Motion Matching
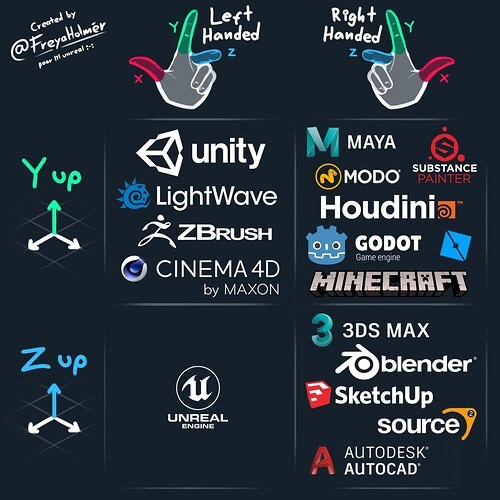
Common Software Coordinate Systems
Rooms and Mazes: A Procedural Dungeon Generator
Games for Windows and the DirectX SDK blog
History of Computer Animation
DirectX Documentation
Explosive old news, full of energy: DirectX engineering specs published!
It makes up for the poorly written DX12 documentation: DirectX-Specs
Dragon Book DirectX12 GitHub link: d3d12book
Dragon Book DirectX12 author’s website (the Chinese version seems to lack a CD; you can find missing images from the exercises in the DX11 version resources on this site): http://d3dcoder.net/
DX12 Microsoft GitHub example: DirectX-Graphics-Samples
D3D documentation (though the DX12 section is poorly written…): windows/desktop/direct3d
DirectXMath library: DirectXMath
DirectX texture library (DirectXTex): DirectXTex
Microsoft open-source shader compiler: DirectXShaderCompiler
walbourn’s GitHub also has some good stuff like D3D project templates, etc.: walbourn
PIX blog and download link:
https://blogs.msdn.microsoft.com/pix/
https://blogs.msdn.microsoft.com/pix/download/
DirectX 12 DirectXTK12 (DirectX Tool Kit): https://github.com/Microsoft/DirectXTK12
DirectXMesh geometry processing library: https://github.com/Microsoft/DirectXMesh
DirectX Tool Kit usage demonstration: https://github.com/walbourn/directxtk-samples
DX blog, latest news: https://blogs.msdn.microsoft.com/directx/
Direct3D feature levels discussion (detailed discussion on feature levels): https://forum.beyond3d.com/threads/direct3d-feature-levels-discussion.56575
Around Windows 10 DirectX 11 Platform
- DirectX 11.x DirectXTK (DirectX Tool Kit): https://github.com/Microsoft/DirectXTK
- Direct3D 11.x DXUT: https://github.com/Microsoft/DXUT
- Effects for Direct3D 11 (FX11): https://github.com/Microsoft/FX11
RoadMap
- Clayman “Game Programmer Training Plan”: http://www.cnblogs.com/clayman/archive/2009/05/17/1459001.html
- Milo Yip “The Learning Path for Game Programmers (Chinese and English)”: https://miloyip.github.io/game-programmer/
Dragon Book DX12 Errata
Chinese version P30, exercise 1.8, question 5:
5. Let k be a scalar, vector $u=(u_x,u_y,u_z)$. Prove that $\left| \left| k \right| \right|\left| \left| u \right| \right|$.
The Chinese version has an error here: $\left| \left| k \right| \right|\left| \left| u \right| \right|$ cannot take the norm for a scalar. The original English version is $\left| k \right|\left| \left| u \right| \right|$
Left-Hand Coordinate System and Right-Hand Coordinate System
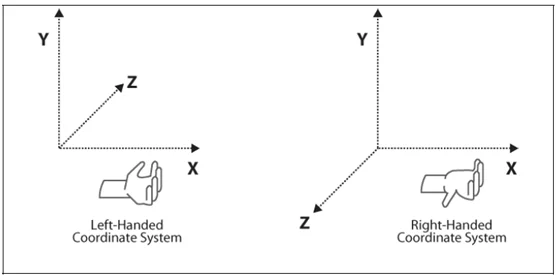
The conversion between left and right-handed coordinate systems only requires reversing one axis (if both axes are reversed, it’s the same as not reversing at all).