Recently, I’ve been intrigued by the mathematical models in computers discussed in “The Beauty of Mathematics” and the number theory from “What is Mathematics.” Today, I managed to suppress my laziness for a moment, and I’m going to analyze the mathematical models in cryptography!
We base our analysis on the basic characteristics of the RSA encryption algorithm (which is also a commonality among many encryption algorithms):
- They have two completely different keys, one for encryption and one for decryption.
- Two seemingly unrelated keys are mathematically linked.
Now, we first use a relatively simple RSA algorithm to illustrate the principle of public keys and encrypt and decrypt Vision.
First, let’s turn Vision into a string of numbers, using its ASCII values as an example:
$$X=086105115105111110$$ (each three digits represent a letter) as plaintext, and design a cryptographic system for this plaintext.
Find two large prime numbers $P$ and $Q$, the larger the better, for example, 100 digits long, and calculate their product (the larger the number, the harder it is to factor).
$N=P\times Q$
$M=(P-1)\times (Q-1)$Find an integer $E$ that is coprime to $M$ (coprime means $M$ and $E$ share no common factors other than 1).
Find an integer $D$ such that $E\times D\ mod\ M=1$ (Fermat’s Little Theorem).
Fermat’s Little Theorem: If $p$ is a prime number that does not divide the integer $a$, then:
$$a^{p-1} \equiv 1 \ (mod \ p)$$
Now a cryptographic system has been designed. Here, $E$ is the public key (used for encryption), and $D$ is the private key (used for decryption), with the product of the public key and secret key $N$ being public.
Now we encrypt the data:
$$X^E\ mod\ N=Y$$
Encryption is complete! Without the key $D$, even a celestial being cannot decrypt $X$ from $Y$ (the computational load is too great, factoring $P$ and $Q$ from $N$ can take many years).
Using the key, one can easily obtain $X$ from $Y$:
$$Y^D\ mod\ N=X$$
The basic flow is as follows: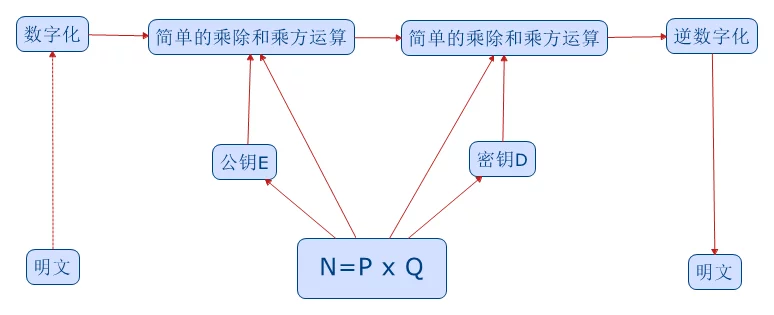
We can see the benefits of public key encryption:
- Simple, it’s just some multiplication and division.
- Reliable, it’s very difficult to reverse engineer; the public key can only be used for encryption, and once encrypted, it cannot be decrypted without the secret key.
- Flexible, it can produce many combinations of public keys and private keys for different encryptors.
There is no password that cannot be cracked; the key is how long it can remain unbroken.
To break public key encryption, the most effective method so far remains to factor $N$, to reverse engineer $P$ and $Q$ from $N$. This is also the reason $N$ and $Q$ must find very large prime numbers, as the importance of prime numbers lies in the fact that: every integer can be expressed as a product of primes, and apart from permutation, the prime factorization of a number $N$ is unique. This means that among all the prime factors of the large number $N$, one must combine $P$ and $Q$ such that $P\times Q=N$. Since the selected $P$ and $Q$ are extremely large primes, this computational load is unimaginable; even if one uses a computer to exhaustively enumerate every possibility, it would take a very long time, in essence, it’s a battle of computational speed.
In summary: the most important concept used in encryption operations is prime numbers; this is fundamental to encryption algorithms due to their difficulty in factorization.
A lot of mathematical knowledge is like this; it may seem not very useful, but in reality, it has great value. Take search engines as an example, at its core, it’s also boolean operations, but it also involves a lot of technology.
Final remark: Mathematics is best when applied!
References
“The Beauty of Mathematics” (Inspired by the drama “Dark Calculation” — Discussing the principles)
“What is Mathematics: A Fundamental Study of Thought and Methods” (Prime number chapter)

