使用Gprof分析代码性能瓶颈

Using profiler to analyze the performance of code is more efficient, detailed, and intuitive than pure cognitive analysis.

Gprof is one of the GNU binutils tools. It can analyze the number of calls to each function in the code and the processor time consumed by each function.

For more information about gprof, you can refer to these two articles: Introduction and Usage of gprof and One of the Linux performance evaluation tools: gprof.

Here, let’s simply discuss how to use gprof (for more parameters, you can check the above blog):

1. When compiling code with G++, the -pg parameter must be added.
2. After compilation, run the generated .exe file, which will create a gmon.out file.
3. Export the analysis results: gprof -b runFileName.exe gmon.out > result.txt.

Actually, to make it convenient, I used gprof (-pg parameter) in the Build System of my Sublime Text while compiling with G++. You can check my Sublime Text configuration here: Configuring Sublime Text as a Lightweight IDE for C/C++.

Now let’s practice using gprof to analyze code:

Let’s take an example of outputting prime numbers within N.

A prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers, or in other words, a number that has exactly two distinct positive divisors: one and itself. — Wikipedia

First, we will write a piece of code, based on the definition of a prime number. The simplest way to check if a number N is prime is to check the remainder when dividing N by every integer from 2 to N-1. If there exists any integer that divides N evenly, we can conclude that it is not a prime number.

The code is as follows:

// Find all prime numbers within 1000
bool prime(int n){
	for (int i = 2; i < n; ++i){
		if(n % i == 0)
			return false;
	}
	return true;
}
int main(void)
{
	int n = 1000;
	// Count the number of prime numbers within N
	int index = 0;
	for (int i = 2; i < n; ++i){
		if(prime(i)){
			printf("%d\t", i);
          	 ++index;
		}
	}
  	printf("\nThe number of prime numbers within %d to %d\n", n, index);
	return 0;
}

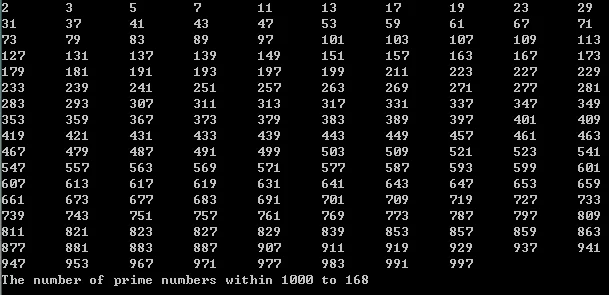
A total of 168 prime numbers were found within 1000.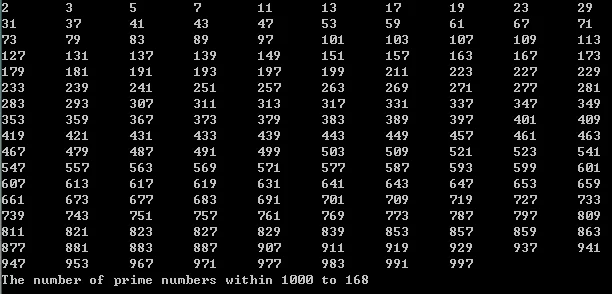

Now, let’s analyze it with gprof: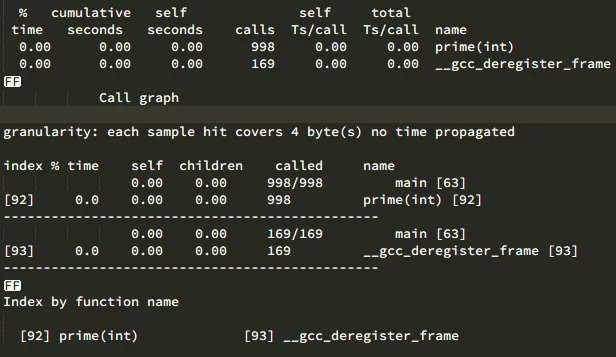

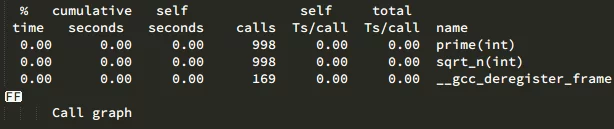
We can see that prime was called 998 times (because it’s about numbers within 1000).

This algorithm is a very naive brute force approach (from 2 to N). Let’s optimize this algorithm.

Deterministic Algorithm: Sieve of Eratosthenes (another type of trial division)

Try to check integers from 2 to $\sqrt{N}$ to see if they divide N evenly, to determine if N is prime.

The modified code is as follows:

int sqrt_n(int n){
	return (int)sqrt((float)n);
}
bool prime(int n){
	for (int i = 2; i <= sqrt_n(n); ++i){
		if(n % i == 0)
			return false;
	}
	return true;
}
int main(void)
{
	int n = 1000;
	for (int i = 2; i < n; ++i){
		if(prime(i)){
			printf("%d\t", i);
		}
	}
	return 0;
}

Now let’s analyze it with gprof again:

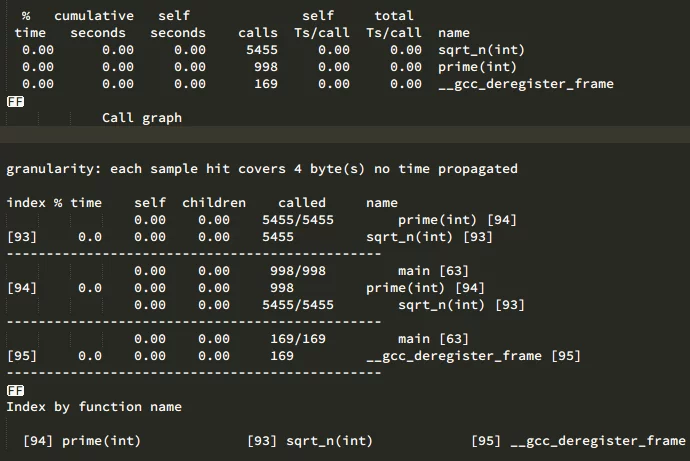
We can see that prime was called 998 times and sqrt_n was called 5455 times (a total of 5455 sqrt operations on n).

One particularly important point to note is this line of code:

for (int i = 2; i <= sqrt_n(n); ++i)

This loop calls sqrt_n once for each iteration, resulting in the prime function calling sqrt_n N times for each N processed. However, sqrt_n only needs to be called once for its role within prime, so we can modify the code to:

int tmp = sqrt_n(n);
for (int i = 2; i <= tmp; ++i)

How to optimize again?

Consider the testing order as follows:

2 3 4 5 6 7 8 9 10 11 12 13 14 …… N-1

Among them, 4, 6, 8, 10, 12, 14 … are all multiples of 2, so we can replace the remainder check of these numbers with N % 2.

Additionally, 9, 15, 21, 24 … are multiples of 3, so we can replace these numbers with N % 3.

Similarly, for multiples of 5, we can directly check the remainder of N against these bases; if it equals 0, then it is a composite number, otherwise, it is a prime number.

// Add checks for 2, 3, and 5 to the prime function
bool prime(int n){
	if(n % 2 == 0) { return false; }
	if(n % 3 == 0) { return false; }
	if(n % 5 == 0) { return false; }
	int tmp = sqrt_n(n);
	for (int i = 7; i <= tmp; ++i){
		if(n % i == 0)
			return false;
	}
	return true;
}

Analysis results: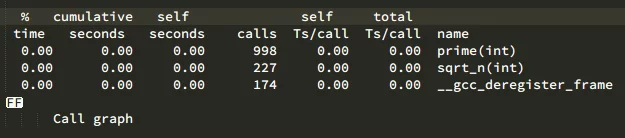

We can see that the number of calls to sqrt_n dropped to 227.

However, there was a problem with the above code:

Run results: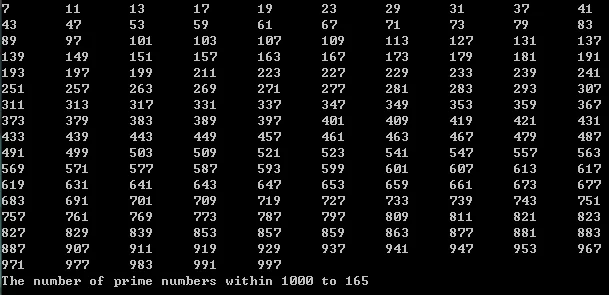

Only 165 prime numbers were found within 1000, while our exhaustive search (the first code) yielded 168.

From the screenshot of the run results, we can see that 2, 3, and 5 are missing from the list because when n = 2, 3, or 5, the function returns false. Therefore, we need to add a few conditional statements to the return expression:

// If N equals 2, 3, or 5, return true
if(n % 2 == 0) { return n == 2; }
if(n % 3 == 0) { return n == 3; }
if(n % 5 == 0) { return n == 5; }

Run again: